A collection of Constraint Programming models for the three-dimensional stable matching problem with cyclic preferences
Ágnes Cseh, Guillaume Escamocher, Begüm Genç & Luis Quesada
Abstract
We introduce five constraint models for the 3-dimensional stable matching problem with cyclic preferences and study their relative performances under diverse configurations. While several constraint models have been proposed for variants of the two-dimensional stable matching problem, we are the first to present constraint models for a higher number of dimensions. We show for all five models how to capture two different stability notions, namely weak and strong stability. Additionally, we translate some well-known fairness notions (i.e. sex-equal, minimum regret, egalitarian) into 3-dimensional matchings, and present how to capture them in each model. Our tests cover dozens of problem sizes and four different instance generation methods. We explore two levels of commitment in our models: one where we have an individual variable for each agent (individual commitment), and another one where the determination of a variable involves pairing the three agents at once (group commitment). 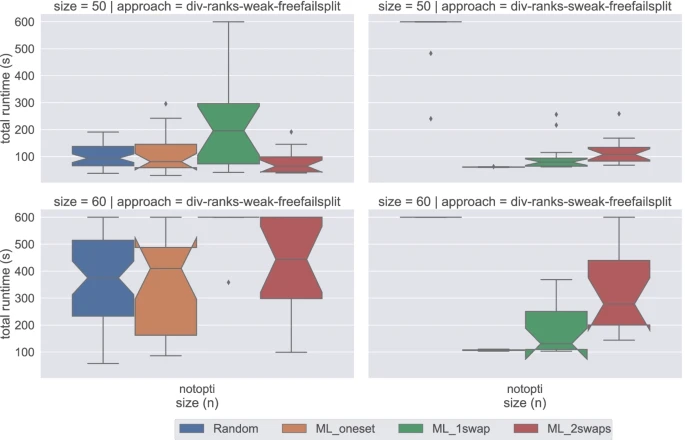 Our experiments show that the suitability of the commitment depends on the type of stability we are dealing with, and that the choice of the search heuristic can help improve performance. Our experiments not only brought light to the role that learning and restarts can play in solving this kind of problems, but also allowed us to discover that in some cases combining strong and weak stability leads to reduced runtimes for the latter.
Our experiments show that the suitability of the commitment depends on the type of stability we are dealing with, and that the choice of the search heuristic can help improve performance. Our experiments not only brought light to the role that learning and restarts can play in solving this kind of problems, but also allowed us to discover that in some cases combining strong and weak stability leads to reduced runtimes for the latter.
Keywords
- Three-dimensional stable matching with cyclic preferences
- 3DSM-cyc
- Constraint programming
- Fairness



