Partitioned matching games
for international kidney exchange
Márton Benedek, Péter Biró, Walter Kern,
Dömötör Pálvölgyi & Daniel Paulusma
Mathematical Programming – Published:
Abstract
We introduce partitioned matching games as a suitable model for international kidney exchange programmes, where in each round the total number of available kidney transplants needs to be distributed amongst the participating countries in a “fair” way. A partitioned matching game ( N , v ) is defined on a graph G=(V,E) G = ( V , E ) with an edge weighting w and a partition V=V_1 \cup \dots \cup V_n V = V 1 ∪ ⋯ ∪ V n . The player set is N = \{ 1, \dots , n\} N = { 1 , ⋯ , n } , and player p \in N p ∈ N owns the vertices in V_p V p . The value v ( S ) of a coalition S \subseteq N S ⊆ N is the maximum weight of a matching in the subgraph of G induced by the vertices owned by the players in S . If |V_p|=1 | V p | = 1 for all p\in N p ∈ N , then we obtain the classical matching game. Let c=\max \{|V_p| \; |\; 1\le p\le n\} c = max { | V p | | 1 ≤ p ≤ n } be the width of ( N , v ). We prove that checking core non-emptiness is polynomial-time solvable if c\le 2 c ≤ 2 but co–hard if c\le 3 c ≤ 3 .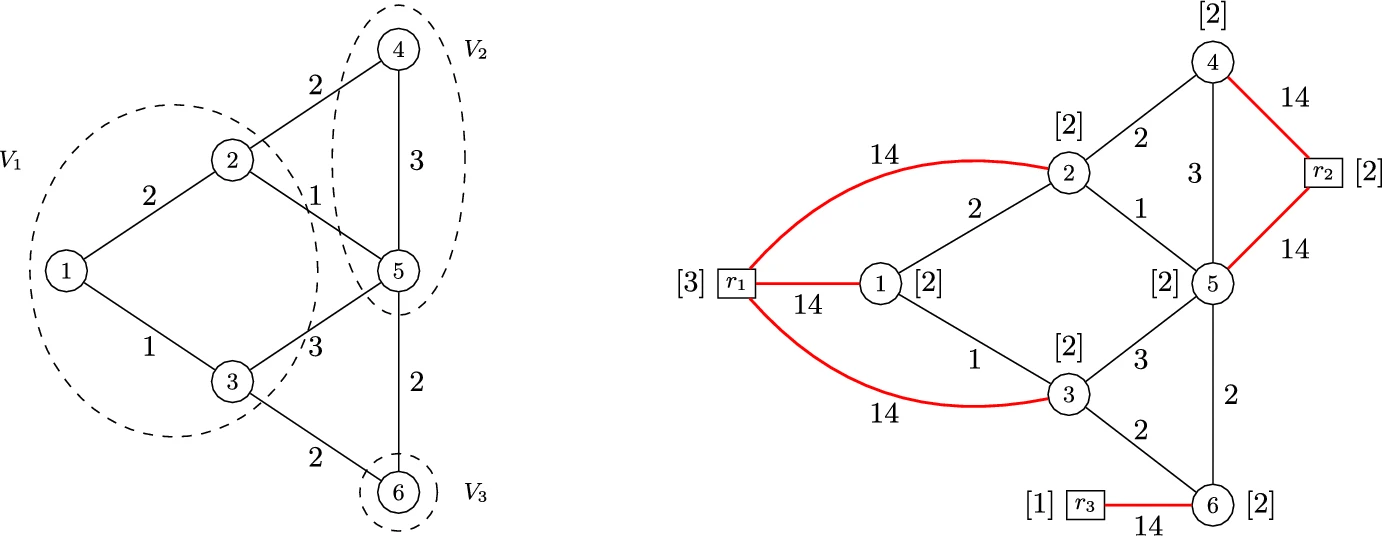 
We do this via pinpointing a relationship with the known class of b -matching games and completing the complexity classification on testing core non-emptiness for b -matching games. With respect to our application, we prove a number of complexity results on choosing, out of possibly many optimal solutions, one that leads to a kidney transplant distribution that is as close as possible to some prescribed fair distribution.
Download PDF
